ろびこ「秘密の恋３ ビー玉の橋」
講談社『デザート』2008年4月号
眼鏡っ娘起承転結構造が美しい短編。
主人公のノブコさんは、自分に自信が持てない眼鏡っ娘女子高生。サッカー部の市井くんを好きになるが、告白なんてできっこない。そこで、ビー玉が埋め込まれた橋からビー玉を削り取ろうとしていた。「ビー玉を掘り出すと恋が叶う」という都市伝説が地元にあったのだ。眼鏡っ娘がビー玉を削り取ろうとしているところに、中学校の同級生、八木くんが通りかかった。
後ろ向きな眼鏡っ娘を八木くんが元気づける。八木くんに励まされた眼鏡っ娘は、片想いの市井くんにアタックするために努力することを決意する。しかし残念なことに、間違った方向に努力をしてしまう。なんと眼鏡を外してコンタクトにしてしまうのだ！ガッデム！！
眼鏡を外したノブコに、市井くんが話しかけて、とてもいい感じ。天にも昇るような気持ち。しかしこれまで本コラムを読んできた方は、眼鏡を外していい感じになった気がしても、最後には必ず裏切られることを既にご存じのはずだ。それが世界の摂理だからだ。案の定、本作でも世界の法則はしっかり守られる。
ノブコの間違った方向への努力は当然実ることなく、市井くんはあっさり別の女とくっついてしまうのだった。そしてさらに、ノブコはそのことにあまりガッカリしていない自分に気が付く。「あんまり好きじゃなかったのかな」とも思う。そしてコンタクトに何も意味がなかったことに気が付き、再び眼鏡をかける。
再び眼鏡をかけたノブコは、八木くんとビー玉の橋で会う。そこで八木くんは、ビー玉を削り取って眼鏡っ娘に渡し、告白する。眼鏡っ娘も、実は八木くんのことを好きだった自分に気が付く。眼鏡をかけて、ようやく自分の気持ちに気が付くことができたのだ。
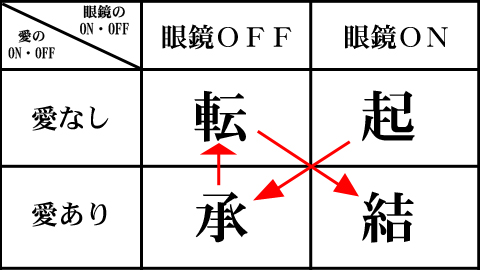というわけで、本作のプロットは典型的な「眼鏡っ娘起承転結構造」となっている。が、もちろん過去の作品とは雰囲気は大きく異なっている。絵柄、コマ割り、ネームなど、実に洗練されたハイセンスな画面構成だ。しかしそれでも、「眼鏡っ娘起承転結構造」というプロットが共通していることが、決定的に重要な事実である。1970年代半ばの乙女チック時代に完成した「眼鏡っ娘起承転結構造」が、21世紀になってからのハイセンスな作品でも極めて高い説得力を持つことを、本作は雄弁に示している。
「眼鏡っ娘起承転結構造」が時代を超えた普遍的な説得力を示し続けるのは、時代に左右されない盤石な哲学的裏付けを持っているからだ。ヘーゲル弁証法に基づいた哲学的裏付けに関しては機会を改めて解説することとしたいが、具体的な作品として21世紀にも「眼鏡っ娘起承転結構造」が見られることは事実として確認しておきたい。
■書誌情報
本作は42頁の短編。単行本『ひみこい』第１巻に所収。『ひみこい』は全２巻だが、一話読み切りのオムニバス形式なので、本作だけ読む場合は１巻だけで話が通じる。
| ■広告■ |
| ■広告■ |
